どのレースが荒れやすい?競艇出場選手のクラスから考えるレース傾向
ボートレースでは選手がA1からB2まで4つのクラス(級別)に分かれており、半年ごとにその期の成績によって競艇のレーサーとしてのクラスが決まります。
SGやG1といったグレード戦では、一番上のクラスであるA1のレーサーたちで出場選手枠が埋められますが、一般戦になると各クラスからレーサーが集まり、同じレースでクラスの異なる選手たちが戦います。
レースを予想して楽しむ私たちにとっては、同じクラスの選手が集まったレースとそうでないレースのどちらが固い決着(人気のある組み合わせ)になりやすいのか、どちらが荒れやすいのか、という傾向を知っておくことは重要です。
この記事では、2021年11月から2022年5月のレース結果のデータを使って、レースに出場する選手のクラスのばらつき具合(または集中度合い)によってレース結果にどのような傾向があるのか、3連単の確定オッズの観点から比較します。
自分の予想スタイルやベットする傾向、あなたが本命派なのか穴党なのかによって、ベットするのに適したレースとそうでないレースというものがあります。今日はどのレースを楽しもうか、とベットするレースを決める際にぜひ参考にしてください。
結論はこちらから >> 【結論】出場選手のクラスの偏り度合いと確定オッズの関係
分析の流れ:クラスを点数化してレースごとの級別偏り・オッズの関係を明らかにする
一つのレースに出場するボートレーサーのクラス(級別)のばらつき具合によってレース結果にどのような傾向が現れるのかを分析するために、まずはクラスごとの「重み」を決めます。
クラスのばらつきは出場する6選手のクラスの偏差を計算して比較しますが、そのときに各クラスに点数(数字)を割り当てる必要があります。その数字(重み)をどう設定しようか、というのが最初のタスクです(データ分析1)。
レーサーのクラスに重み付け(点数化)ができたら、次にレースごとの出場選手のクラス偏差(偏り度合い)ごとにレース結果の3連単オッズを比べます(データ分析2)。
3連単オッズの分析は、レースのクラス偏り度合いごとにオッズの平均(調和平均)とオッズの偏差を計算します(データ分析3)。オッズの偏差というのは、オッズのばらつきを意味するので、その値が大きいほど「オッズが安定しない」=「高いオッズが出ることがある」ということを示唆します。
データ分析1:クラスの重み付けで力関係を数値化する
まずはA1からB2のクラスの重み付けをおこなっていきます。
クラスの重み付けは、クラスに対して何点を付ければその点数とレース結果(順位)の相関関係が高くなるか、という分析をおこなって決めます。
例えば仮に、
A1クラス:4点、A2クラス:3点、B1クラス:2点、B2クラス:1点
と重み付けすれば、各クラスは均等に点数化された状態になります。
こうやって点数化することで、
クラスが偏っている・集中しているレース
1 A1 4点 2 A1 4点 3 A2 3点 4 A1 4点 5 A2 3点 6 A1 4点
クラス平均: 3.67点 クラス偏差: 0.47
クラスがばらついているレース
1 A1 4点 2 B2 1点 3 A2 3点 4 A1 4点 5 B1 2点 6 B2 1点
クラス平均: 2.50点 クラス偏差: 1.26
といった具合でレースごとのクラスの偏り度合いを数値化して比較できます。
上の例ではA1からB2まで均等に点数を設定しましたが、本当にそれでいいのでしょうか?
均等な点数化だと、A1とA2クラスの差はA2とB1・B1とB2のクラス差と同じ程度の差ということになります。もしもB1とB2の差をA1とA2の差よりも大きくした方がクラス間の力量差をうまく表すことができるというなら、点数の付け方にそういった力の差を反映させるべきです。
今回は、A1:10点、B2:0点というように上と下の点数を固定して、A2とB1の点数パターンごとにレース結果順位との相関関係(ピアソンの相関係数)を計算しました。調査する点数パターンは以下の36パターンです。
| B2 | B1 | A2 | A1 |
|---|---|---|---|
| 0点 | 1点 | 2点 | 10点 |
| 0点 | 1点 | 3点 | 10点 |
| 0点 | 1点 | 4点 | 10点 |
| 0点 | 1点 | 5点 | 10点 |
| 0点 | 1点 | 6点 | 10点 |
| 0点 | 1点 | 7点 | 10点 |
| 0点 | 1点 | 8点 | 10点 |
| 0点 | 1点 | 9点 | 10点 |
| 0点 | 2点 | 3点 | 10点 |
| 0点 | 2点 | 4点 | 10点 |
| 0点 | 2点 | 5点 | 10点 |
| 0点 | 2点 | 6点 | 10点 |
| B2 | B1 | A2 | A1 |
|---|---|---|---|
| 0点 | 2点 | 7点 | 10点 |
| 0点 | 2点 | 8点 | 10点 |
| 0点 | 2点 | 9点 | 10点 |
| 0点 | 3点 | 4点 | 10点 |
| 0点 | 3点 | 5点 | 10点 |
| 0点 | 3点 | 6点 | 10点 |
| 0点 | 3点 | 7点 | 10点 |
| 0点 | 3点 | 8点 | 10点 |
| 0点 | 3点 | 9点 | 10点 |
| 0点 | 4点 | 5点 | 10点 |
| 0点 | 4点 | 6点 | 10点 |
| 0点 | 4点 | 7点 | 10点 |
| B2 | B1 | A2 | A1 |
|---|---|---|---|
| 0点 | 4点 | 8点 | 10点 |
| 0点 | 4点 | 9点 | 10点 |
| 0点 | 5点 | 6点 | 10点 |
| 0点 | 5点 | 7点 | 10点 |
| 0点 | 5点 | 8点 | 10点 |
| 0点 | 5点 | 9点 | 10点 |
| 0点 | 6点 | 7点 | 10点 |
| 0点 | 6点 | 8点 | 10点 |
| 0点 | 6点 | 9点 | 10点 |
| 0点 | 7点 | 8点 | 10点 |
| 0点 | 7点 | 9点 | 10点 |
| 0点 | 8点 | 9点 | 10点 |
出場するレーサーのあいだでクラスが上の選手ほど順位がよくなる傾向があるだろうというのは自然に予想が付きます。
重み付けの点数パターンごとに順位との関係性を数値化して、一番いい点数パターンを選択したなら、そのパターンは他のパターンに比べて選手の力量差(順位が上になる具合)をうまく反映しているだろう、というのがこの話しの流れです。
クラスと順位の相関関係の値(相関係数)の絶対値は0から1の範囲に収まり、値が大きいほど関係性が強いということになります。
対象期間(2021年11月から2022年4月)のレースデータを使って、クラス点数とレース順位の相関関係の値を見ると、
B2:0点・B1:5点・A2:8点・A1:10点
というパターン(相関係数:0.373)を採用するのが一番よさそうです。
この重み付けのパターンは、B1とB2のクラス間の力量差が一番大きく(5点)、A1とA2の力の差(2点)よりはA2とB1の差の方が少し大きい(3点)、ということを示しています。恐らく多くの方が抱くクラスに対するイメージに近い結果となっているのではないでしょうか。
ちなみに、均等に点数付けしたときの値が0.365で、オレンジ色の線で表示されています。
参考までに、選手ランクを決める元になっている勝率と順位の相関関係は0.376。出場選手の勝率の標準得点(出場する6選手間の比較)を使うと、0.429となります。
- クラスの点数は、点数をそのまま使うのではなく、同じレースの出場選手間で選手のクラスが他の選手に比べてどれだけ高いかを表す標準得点を使ってレース結果順位との相関関係を調べています。
- 対象のレースは、2021年11月から2022年4月まで。出場選手のクラスがA1に限定されるSG・G1レースは対象から除きました。また、6艇が完走していないレース(欠場やフライング・転覆などが発生したレース)も除外しました。
- 選手のクラスは2021年11月時点。
データ分析2:クラスの偏り度合いとオッズの関係を描写する
クラスごとの点数(重み付け)が決まったところで、レースのクラスばらつき具合とレース結果の3連単オッズの関係を見ていきましょう。
出場するレーサー6名のクラスに対して、クラスの点数の標準偏差をそのレースのクラス偏り度合い(または集中度合い)とします。
偏り度合いが0ならば6人が全員同じクラス。選手のクラスがばらばらで、特にA1とB2の選手が混合しているようなレースは標準偏差が大きくなる、といった具合です。
クラスが偏っている・集中しているレース
1 A1 2 A1 3 A1 4 A1 5 A1 6 A1
クラス偏差:0 レース結果・3連単オッズ:1 – 2 – 4 1,990円
クラスがばらついているレース
1 B1 2 A1 3 A2 4 A2 5 B1 6 B2
クラス偏差:3.21 レース結果・3連単オッズ:2 – 4 – 1 1,220円
横軸に出場選手のクラス偏差、縦軸にレース結果の3連単オッズとしてプロットしたグラフがこのようになります。
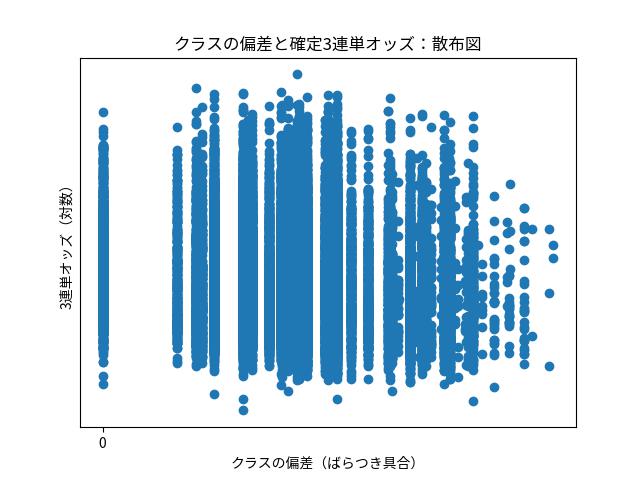
※3連単オッズはプロットしやすいよう逆数の対数(絶対値)を取っています
一番左の縦に集まっているのが、クラス偏差が0、つまり出場選手が全員同じクラスのレースです。
少し離れた縦軸の2つ目が、5人A1・1人A2のレース(またはその逆で5人A2・1人A1)、次が5人A2で1人B1というように、横軸は飛び飛びの値になっています。
上の方がオッズが高い決着(荒れた結果)、下の方がオッズが低い決着ということを示していますが、これだけだとわかりにくいですね。
近い値のものをまとめて、含まれる数でプロットの大きさを変えたバブルチャートも載せておきます。
数の多い中心部に比べると、左側の方(出場選手クラスのばらつきが少ない方)がオッズのばらつきが若干小さめかも、という感じでしょうか。
中心部と比べると右側はオッズが低い部分の割合が多くなっているかもしれませんが、右側は比較的数が少なく、はっきりとした傾向というのは見えてきません。
クラスの偏り度合いとレース結果の確定オッズの関係を描写できたので、次ではクラス偏り度合いを区切って、区切られた範囲に含まれるレースの平均オッズ(レース結果の3連単オッズ調和平均)とオッズのばらつき具合を見ていきます。
データ分析3:クラスの偏り度合いと平均3連単オッズ・オッズのばらつき
レースごとの出場選手クラス偏差を区切って、区切られた範囲内に入るレースの確定3連単オッズを比べます。
一つの区切られた範囲のレース数が少ないと、結果が荒れたレースが少し含まれるだけで大きく数値がぶれてしまうため、一つの区切りには100レース以上が含まれるように範囲を調整しています。
横軸がクラスの偏り度合いなので、一番左が全員同じクラスの場合、右に行くほど出場する選手のクラスがばらばらになっています。
この分析ではしっかり傾向が出ましたね。
確定3連単のオッズは、クラスの偏りがない(出場選手全員が同じクラス)場合に一番高く、23.4倍。クラス偏差が大きくなるに従って平均オッズは下がり、一番低いところでは13.0倍となっています。
これで単純にクラスが同じ選手が集まったレースの方が荒れやすい、ということにはならないようで、同じグラフに折れ線グラフで描かれた確定3連単オッズの標準偏差は逆の傾向を示しています。
つまり、右にいくほど(クラスがばらばらなほど)平均オッズは下がる傾向があるが、「オッズ倍率がばらばらな値を取る頻度が増える」=「レース結果が荒れる(3連単のオッズが高く付く)頻度が増える」ということのようです。
結論:同じクラスに集中するほど平均オッズは高くなるけれど…
これまで見てきた結果、あるレースの出場選手のクラスについて、
クラスが集中しているほど、
①平均の確定3連単オッズは高くなる
②オッズの偏りは小さく、大きく荒れる頻度は比較的少ない
クラスが散らばっている(ばらばら)ほど、
①平均の確定3連単オッズは小さくなる
②オッズの偏りは大きく、大きく荒れる頻度が比較的多い
ということがわかりました。
実力が拮抗しているレースはどの選手にも複勝圏に入ってくる可能性があるので3連単のオッズが全体的に高くなり、実力の差がはっきりしている場合は特定の組み合わせに人気が集中する、と考えれば①の平均確定3連単オッズの傾向は説明できそうです。
そうは言っても、結果のグラフを見ると平均オッズの最小は13.0倍から23.4倍まで。意外と差が大きいものだと私は感じましたが、これを見たあなたはいかがだったでしょうか。
もしも私と同じように感じていて、あなたがオッズによってベットする組み合わせを調整する予想スタイルであれば、ある3連単の倍率がレース出場選手のクラス集中度合いによって高いか低いか変わってくるということを知っていることは、あなたにとって有用な知識になるはずです。
クラスの偏り度合いとオッズの関係を予想に活かす BKCボートレース予想用データ分析
BKCのボートレース情報では、全レースの出場選手クラス分布を毎日紹介しています。
予想用データ分析ページでは、逃げ成功見込みや進入変化発生見込みに加えて、レース開催場ごとの出場選手クラス割合というものが掲載されています。
開催上別クラス分布比較のサンプルです。
>>ボートレース予想用データ分析 2022年5月26日開催 逃げ成功見込み・出場選手クラス情報
開催場別の出場選手クラスで紹介しているデータは、全12レースに出場するレーサーのクラスがどのような割合になっているかをチェックできます。
これらのデータを活かして、どのボートレース場でベットするのかを決める際に自分の予想スタイルにあう開催を選択できれば、回収率にいい影響が現れるでしょう。
また、レースの一覧では、各レースの出場選手クラスも掲載されています。
クラスの偏り度合い・集中度合いによってベットのターゲット(対象レース・買い目)を調整することも、回収率を高める一因になりえるでしょう。
>>毎日更新 BKCボートレース予想用データ分析
あなたがボートレースをより楽しめるよう、BKCが貢献しますように。
- 今回の分析では、出場レーサーのクラスが限定されるSG・G1レースを除いています。平均オッズが23.4倍となった出場レーサーが全員同じクラスのパターンには、SG・G1のレースは含まれていないので注意してください。
ご意見・ご要望など、ぜひこちらの問い合わせフォームからお送りください。ご指摘であったり、こんな分析データを見たいといった要望など、何でも歓迎します。

